卡米拉Cziráki是Eötvös Loránd大学(ELTE)科学系地球物理学专业的一名学生,她采用了一种新的方法来研究导航系统,该系统可以用于月球表面,以规划未来的旅行。
与地球物理和空间科学系负责人Gábor Timár教授合作,Cziráki使用800年前数学家斐波那契的方法计算了地球卫星定位系统中使用的月球参数。他们的研究结果发表在《地球物理学报》上。
现在,随着人类准备在半个世纪后重返月球,人们关注的焦点是月球导航的可能方法。现在看来,阿波罗登月任务的现代接班人很可能会得到某种形式的卫星导航的帮助,类似于地球上的GPS系统。以地球为例,这些系统没有考虑地球的实际形状,即大地水准面,甚至没有考虑海平面定义的表面,而是考虑最适合大地水准面的旋转椭球体。
它的交点是一个椭圆,在赤道离地球质心最远,在两极离地球质心最近。地球的半径不到6400公里,两极距离地心的距离比赤道近21.5公里。
为什么最适合月球的椭球体的形状很有趣,什么参数可以用来描述它?月球的平均半径为1737公里,相比之下,它的两极离质心的距离比离赤道的距离近半公里,这是为什么有趣呢?如果我们要将GPS系统中尝试和测试的软件解决方案应用到月球上,我们需要指定这个椭球体的半长轴和半短轴两个数字,这样程序就可以很容易地从地球转移到月球上。
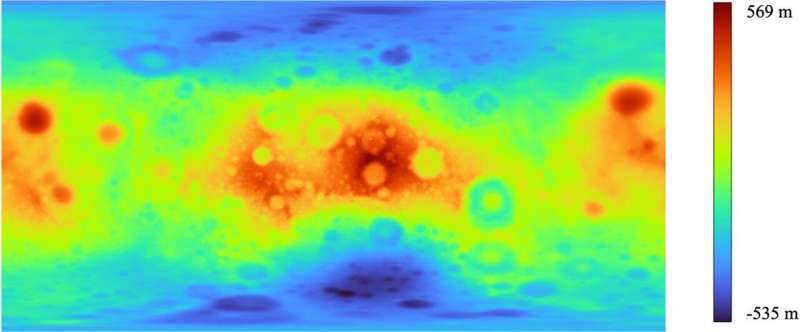
月球的自转速度较慢,其自转周期等于其绕地球公转的周期。这使得月球更圆。它几乎是一个球体,但又不完全是。尽管如此,对于迄今为止所绘制的月球地图来说,仅仅近似于一个球体的形状就已经足够了,那些对我们的天体伙伴的形状更感兴趣的人使用了更复杂的模型。
有趣的是,以前从未有人用旋转椭球体近似月球的形状。上一次类似的计算是在20世纪60年代由苏联太空科学家进行的,他们使用了从地球上可见的月球侧面的数据。
专攻地球物理的地球科学二年级学生Cziráki与她的导师Timár一起计算了最符合月球理论形状的旋转椭球体的参数。
为了做到这一点,他们使用了一个现有的潜在表面的数据库,称为月球面,从中他们在表面上均匀间隔的点上取了一个高度样本,并寻找最适合旋转椭球体的半长轴和半短轴。通过从100个采样点逐渐增加到100,000个采样点,两个参数的值稳定在10,000个点。
这项工作的主要步骤之一是研究如何在球面上均匀排列N个点,并有几种可能的解决方案;Cziráki和Timár选择了最简单的一种,即所谓的斐波那契范围。相应的斐波那契螺旋可以用非常简短和直观的代码来实现,这种方法的基础是由800岁的数学家莱昂纳多·斐波那契奠定的。将该方法应用于地球作为验证,重建了GPS使用的WGS84椭球的良好近似值。
本文来自作者[抬眉见雪]投稿,不代表怀缘榴立场,如若转载,请注明出处:https://m.hy6.cc/cskp/202505-411.html


评论列表(4条)
我是怀缘榴的签约作者“抬眉见雪”!
希望本篇文章《一项历经800年的数学方法或许能助力月球导航》能对你有所帮助!
本站[怀缘榴]内容主要涵盖:国足,欧洲杯,世界杯,篮球,欧冠,亚冠,英超,足球,综合体育
本文概览:...